抽屉原理公式大全(奥数精讲——抽屉原理)
抽屉原理公式大全(奥数精讲——抽屉原理)

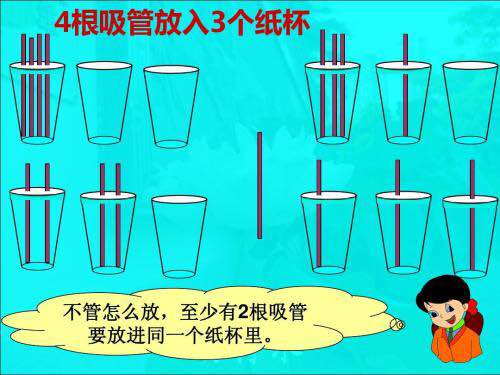
1.把3个苹果放到2个抽屉中,那么至少有1个抽屉中放有2个苹果,把它进一步延伸就可以得到抽屉原理,即:把n+1或多于n+1个物体放到n个抽屉里,其中必定有一个抽屉里至少有2个或2个以上的物体,我们把这种现象称为抽屉原理。
2.抽屉原理的公式:(1)物体数÷抽屉数=商 至少数=商
(2)物品数÷抽屉数=商……余数 至少数=商+1
(3)最少物体数=(至少数-1)×抽屉数+余数
3.用抽屉原理解决问题时,关键是要明白哪些数量是“抽屉”,哪些数量是“物体”,再利用公式解答。

精讲1: 把5个苹果放入4个抽屉里,至少有一个抽屉要放进几个苹果?

解: 5÷4=1(个)……1(个)
1+1=2(个)
答:至少有一个抽屉要放进2个苹果。
精讲2: 把若干条金鱼放进8个鱼缸里,不管怎么放,要保证总有一个鱼缸里至少放进3条金鱼,那么金鱼的总数至少应该是多少条?
分析:最少物体数=(至少数-1)×抽屉数+余数。
解: 8×(3-1)+1=17(条)
答:金鱼最少有17条。

精讲3: 盒子里有5支蓝铅笔和4支红铅笔,要想保证一次能拿出两个同颜色的铅笔,至少要拿出多少支铅笔?
分析:把两种铅笔看作2个抽屉:(1)如果每次拿2支铅笔会有三种情况:①一支蓝铅笔、一支红铅笔;②两支蓝铅笔;③两支红铅笔。这样不能保证一次能拿出两支同颜色的铅笔。(2)如果每次拿3支铅笔会有四种情况:①一支蓝铅笔、两支红铅笔;②一支红铅笔、两支蓝铅笔;③三支蓝铅笔;④三支红铅笔。2+1=3(支)
答:至少要拿出3支铅笔。
精讲4:有红、黄、绿三种颜色的帽子各6顶,装在一个黑色的布袋里,从袋子里任意取出帽子,为确保至少有2顶帽子不同颜色,则至少要取出多少顶帽子?
分析:考虑最坏的情况,若已经取出了一种颜色的全部6顶帽子和其他两种颜色的帽子各一顶,再取出一顶 时,即得到2顶不同颜色的帽子。所以至少要取出 6+2+1=9(顶)。
答:至少要取出9顶帽子。